HELP Edek: HELP! By żyło się lepiej! Dla ludzi lubiących się wykazywać Wykaż, że dla każdej trójki liczb rzeczywistych a, p, q (a≠0) równanie

1		1		1
	+		=		ma pierwiastki rzeczywiste.
x−p		x−q		a2

	a		b
Udowodnij, że jeśli a≠b i a+b =2c to =		+		= 2
	a−c		b−c

	1
Liczby rzeczywiste a, b, c spełniają warunek a+b+c=1. Udowodnij, że ab+bc+ca≤
	3

Mickej: myśle czy mamy się wykazać dla siebie czy ty nie potrafisz tego zrobić i chcesz nas podejść psychologicznie abyśmy to rozwiązali co do 2 i 3 już kiedyś wykazałem a 1 może jak mi się będzie chciało to napisze za godzine jak będe spowrotem

Edek: Dzięki, co do pytania, tak nieumiem

Mickej: tak myślałem ostatnie najtrudniejsze poszukaj w postach było jakies 4 dni temu a 2 piersze wystarczy sprowadzić do wspólnego mianownika

Mickej: co do pierwszego pisze

dpelczar: Mickej mam prosbe

Mickej:

1		1		1
	+		−		=0
x−p		x−q		a2

x−p+x−q		1
	−		=0
(x−p)(x−q)		a2

(x−p+x−q)a2−(x−p)(x−q)
	=0
(x−p)(x−q)a2

−x2+(a2+p+q)x−pa2−qa2−pq
	=0 czyli wystarczy wykazać że licznik ma miejsca
(x−p)(x−q)a2

zerowe −x²+(a²+p+q)x−pa²−qa²−pq=0 delta musi być ≥0 Δ=(a²+p+q)²+4(−pa²−qa²−pq) Δ=a⁴+p²+q²+4a²p+4a²q+2pq−4pa²−4qa²−4pq Δ=4a⁴+p²+q²−2pq Δ=a⁴+(p+q)² a to zawsze większe bądz równe o czyli wykazane z tym że w zadaniu powinna być jeszcze podana dziedzina a skoro jej nie ma to musimy ją sami podać czyli p≠x q≠x

Mickej: jaka ta prośba?

dpelczar: masz gg co za pytanie... na pewno masz... dałbyś mi numer powiem ci o co mi chodzi...

Mickej: gg Hmm ciekawe co to jakiś komunikator? 3444178 ale jak chcesz mnie przelecieć to adresu ci nie podam

dpelczar: nie no nie z tych jestem juz ci pisze o co chodzi...

Mickej: 2)

a		b
	+		=2
a−c		b−c

a(b−c)
	+b=2b−2c
a−c

ab−ac+ab−bc=2ba−2ac+c² ac+bc−2c²=0 c(a+b−2c)=0 podstawiamy pod 2c=a+b c(a+b−a−b)=0 0=0 i cacy zadanie wykazane

Edek: Jeszcze raz wielkie dzięki. Jak mógły ktoś to proszę o pomoc w następnych:

	1		1		1
Wykazać, że jeżeli		;		;		są trzema kolejnymi wyrazami ciągu
	a+b		c+a		b+c

arytmetycznego to b² ;a² ;c² są także kolejnymi wyrazami ciągu arytmetycznego. W ciągu arytmetycznym a_m = n i a_n = m . Obliczyć a_p . Wykazać, że jeżeli w ciągu arytmetycznym spełniony jest warunek s_m/s_n=m²/n² to a_m/a_n = (2m −1)/(2n −1). Wykazać, że jeżeli s_n jest sumą n początkowych wyrazów ciągu geometrycznego to s_n(s_3n−s_2n)=(s_2n−s_n)² Wyraz a₁ i iloraz q nieskończonego ciągu geometrycznego zbieżnego (a_n) n=1,2,… są różnymi pierwiastkami równania2x² − 3x − 2 = 0. Uzasadnić, że a₁+a₂+a₃+...+a₁₀₀<⁴₃ Ja wiem, że tego trochę jest, ale naprawdę jestem słaby w wykazywaniu a chciałbym jak najwięcej przerobić, więc proszę o rozwiązania lub podpoiedzi. Z góry dziękuję

Michał Szczotka:

1		1		2
	+		=
a+b		b+c		c+a

	2
U{b+c+a+b}{(a+b)(b+c)−		=0
	c+a

(2b+c+a)(c+a)−2(a+b)(b+c)
	=0 ułamek równy zero kiedy licznik =0
(a+b)(b+c)(c+a)

2bc+c²+2ac+2ba+a²−2ab−2ac−2b²−2bc=0 c²+a²−2b²=0 c²+a²=2b² więc potrafisz wyciągnąć wnioski nad kolejnymi pomyśle

Michał Szczotka: ok teraz to pomarańczowe 2x²−3x−2=0 jedziemy delta pierwiastki to wiesz chyba jak ja tylko podam ile wyszło Δ=25

	1
x1=−
	2

x₂=2 skoro ciąg geometryczny nieskończony zbieżny to wnioskujemy że |q|<1 czyli nasze

	1
q=−		a a1=2
	2

teraz to 100 elementów które mamy zsumować dzielimy sobie na 2 ciągi bo to jest ciąg którego znak jest zmienny to znaczy że raz jest dodatni a raz ujemny więc my zrobimy z niego sumę 2 ciągów geometrycznych które mają po 50 elementów 1 ciąg a₁=2

	1
q=		to się bierz z tego że bierzemy co drugi wyraz ciągu podstawowego i tylko sume 50
	4

wyrazów wyznacz 2 ciąg a₁=−1

	1
q=		i też tyko sumę a na końcu zsumuj sumę obu ciągów i to koniec zadania jeszcze tylko
	4

	4
porównaj ją z
	3

Michał Szczotka: jade fioletowe

Michał Szczotka: S_n ,S_2n ,S_3n to oznacza że jest to suma n lub 2n lub 3n elementów pewnego ciągu geometrycznego i rozpatrujemy teraz 2 przypadki gdy q=1 i gdzy q≠1 1 Przypadek q=1 S_n(S_n3−S_2n)=na₁(3na₁−2na₁)=(na₁)² (S_2n−S_n)²=(2na₁−na₁)²=(na₁)² więc wykazane dla q=1 2 przypadek q≠1

	1−qn		1−q3n		1−q2n
Sn(Sn3−S2n)=a1*		(a1*		−a1*		) wyciągamy przed
	1−q		1−q		1−q

	1
nawias a1,		a do nawiasu wciskamy (1−qn)
	1−q

	a1
(		)2((1−qn)(1−q3n)−(1−qn)(1−q2n))=
	1−q

	a1
(		)2(q4n+q2n−2q3n)=
	1−q

	a1
(		)2*q2*(1−qn)2=
	1−q

	a1
(		*qn*(1−qn))2
	1−q

	1−q2n		1−qn
(S2n−Sn)2=(a1*		−a1		)2=
	1−q		1−q

	a1
(		((1−q2n)−(1−qn))2=
	1−q

	a1
(		*qn*(1−qn))2
	1−q

Michał Szczotka: chyba dobrze

Michał Szczotka: spadam na grilla jak wrócę to pokombinuje jeszcze

Edek: Wielkie dzięki Michale Szczotko

Michał Szczotka: Zielony i niebieski nie do końca kumam to raczej nie zrobię a juz na pewno nie dzisiaj

@Basia: zielone a_m = a₁ + (m−1)*r a_n = a₁ + (n−1)*r a₁ + (m−1)*r = n /*(−1) a₁ + (n−1)*r = m −a₁ − (m−1)*r = −n a₁ +(n−1)*r = m −−−−−−−−−−−−−−−−−−−−−−−−−−−−− (n−1)*r − (m−1)*2 = m−n r(n−1−m+1) = m−n r(n−m) = m−n = −(−m+n) = −(n−m) r = −1 a₁ + (m−1)*(−1) = n a₁ − m + 1 = n a₁ = n+m−1 a_p = a₁ + (p−1)*r = n+m−1+(p−1)*(−1) = n+m−1−p+1 = n+m−p a_p=n+m−p

Edek: Basia niewiem naprawdę jak na to spadłaś, ale masz rację, tak jest w odpowiedziach. Wielki szcunek dla was Basia, Michał i Mickiej i bardzo dziękuję za pomoc.

Edek: "wpadłaś" nie "spadłaś"

Michał Szczotka: tak dla info Mickej to ja

Edek: Iloczyn pewnych trzech liczb pierwszych równa się ich pięciokrotnej sumie. Co to za liczby?

Mickej: nie wiem jak zapisać liczbę pierwszą gdyby tylko nie chodziło o liczby pierwsze to bym zrobił ale w tym przypadku Edku nie pomogę ci

Damian: Panie BOGDANIE.... ja wysiadam na tym zadaniu zatrzymałem sie na stworzeniu równania i tyle nie wiem tak samo jak Michał jak dalej iść

yu: ∞βΩ∑

Mickej: znalazłem je dla ciebie bo sam byłem ciekaw rozwiązania http://www.matura.pl/tematy.php?przed=mat&temat=m03_r5

Damian: o LOL niezłe zadanko...

Edek: Udowodnij twierdzenie cosinusów Próbowałem i nic :X

Bogdan:

x
	= cosα ⇒ x= b*cosα
b

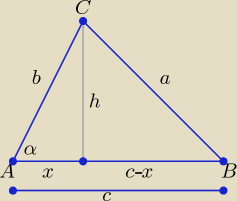
b² = h² + x² ⇒ h² = b² − b²*cos²α a² = h² + (c − x)² ⇒ a² = b² − b²*cos²α + (c − b*cosα)² a² = b² − b²cos²α + c² − 2bccosα + b²cos²α a² = b² + c² − 2bccosα

Edek: Wielkie dzięki

Edek: jeszcze mam tylko parę próśb przed jutrem 1. Udowodnij twierdzenie Ptolemeusza 2. W graniastosłupie prawidłowym trójkątnym poprowadzono płaszczyznę π wyznaczoną przez wysokość dolnej podstawy i ten z wierzchołków górnej podstawy, że płaszczyzna π z płaszczyzną podstawy graniastosłupa tworzy kąt o mierze α ≠ 90⁰. Pole przekroju graniastosłupa wyznaczonego przez płaszczyznę π jest równe S. Oblicz objętość graniastosłupa. 3. Proszę o podpowiedź bo niewiem jak mam narysować wykres y=sin²x ?

Edek: Naprawdę nikt nic Przynajmniej prosiłbym o pierwsze

Jakub: Jeśli chodzi o pierwsze to dowód jest tutaj http://pl.wikipedia.org/wiki/Twierdzenie_Ptolemeusza Jeśli chodzi o trzecie to wejdź na stronkę http://www.jogle.pl/wykresy/ i wpisz y=(sin(x))²

Edek: Serdeczne dzięki